Lately I’m really digging Functional Programming, and especially Haskell. I’ve been reading Real World Haskell, which is a very nice free book about Haskell.

Today I was wondering what Breadth First traversal was. Of course I should know this and it’s stupid I forgot. To make sure I wouldn’t forget in the future I made a little exercise to improve my Haskell skills, and to make sure I wouldn’t forget the Breadth First algorithm anymore.

Depth First and Breadth First are two different ways of traversing a tree. It is best illustrated by the following images from Wikipedia:

Depth First

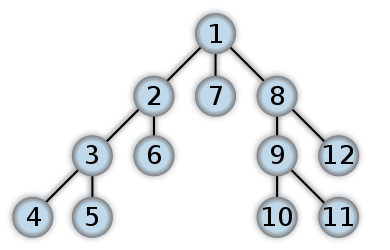
Depth First

source: wikipedia.org

Pseudo (JS) code

Quite simple code

function DFS(G) {
	return [G.value].concat(DFS(G.left), DFS(G.right))
}

Breadth First

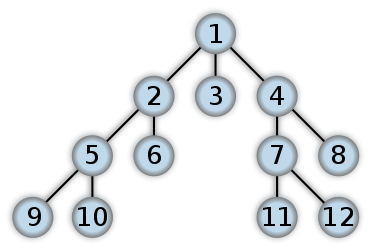
Breadth First

source: wikipedia.org

A bit more complicated code:

function BFS(G) {
	queue = []
	queue.push(G)

	set = []

	while (queue.length) {
		t = queue.shift()
		if (t.left) queue.push(t.left)
		if (t.right) queue.push(t.right)
		set.push(t.value)
	}

	return set
}

Traversal in Haskell

First we have to define a data type for the Tree:

data Tree a = Empty | Node a (Tree a) (Tree a) deriving (Show)

Depth First

The Depth First traversal in Haskell is very easy. If you look at the pseudo code, we can almost directly translate that to Haskell.

traverseDF :: Tree a -> [a]
traverseDF Empty        = []
traverseDF (Node a l r) = a : (traverseDF l) ++ (traverseDF r)

This is simply, concatenate the a with the tree on the left and then on the tree on the right, by recursively calling traverseDF.

Breadth First

Breadth First is more difficult. If you look at the pseudo code there is some queue, which we kind of have to replicate, to make sure that first the root node is added to the resulting set, then the nodes at the first level, second level and finally the leaves.

traverseBF :: Tree a -> [a]
traverseBF tree = tbf [tree]
    where
        tbf [] = []
        tbf xs = map nodeValue xs ++ tbf (concat (map leftAndRightNodes xs))

        nodeValue (Node a _ _) = a

        leftAndRightNodes (Node _ Empty Empty) = []
        leftAndRightNodes (Node _ Empty b)     = [b]
        leftAndRightNodes (Node _ a Empty)     = [a]
        leftAndRightNodes (Node _ a b)         = [a,b]

At tbf [tree] we add the root node to the queue list. Then with map nodeValue xs the values of the nodes of this level are added to the resulting list. Then the tbf function is called again with all the nodes of the next level. The leftAndRightNodes returns a list of the left and/or right nodes of a node. These are concatenated with the other child nodes, and then recursively called with tbf, until all levels of the tree are traversed.

It works!

So now we have two functions, traverseDF and traverseBF, so what are the results. So lets define some tree first:

createTree = Node 'A'
                (Node 'B'
                    (Node 'C' Empty Empty)
                    (Node 'D' Empty Empty)
                )
                (Node 'E'
                    (Node 'F' Empty Empty)
                    (Node 'G' Empty (Node 'H'
                        (Node 'I' Empty Empty)
                        Empty
                    ))
                )

And run this in GHCI:

> let x = createTree
> traverseDF x
"ABCDEFGHI"
> traverseBF x
"ABECDFGHI"

And indeed, these are the results we would expect!

Conclusion

Now I won’t forget which algorithm is which, and I improved my Haskell skills a bit. Of course I did Google/StackOverflow for this problem a little, and should mention this blogpost, which basically the algorithm I used.